PREDICTION CHARTS FROM PRE4CAST
**********************************************************************************************************************************************************************************************************
PREDICTION OF EXTREME PRECIPITATION IN THE SAHEL BASED ON SST INFORMATION FROM THE MEDITERRANEAN AND THE TROPICAL PACIFIC
Extracted from Diakhaté et al. (2020)
Figure 1 - LEFT: Cross-validated skill scores calculated from MCA between forecasts and observations of anomalous Sahelian rainfall calculated in terms of (left column) Pearson correlation coefficients and (right column) root mean square error (RMSE). The analysis is based on the leading MCA calculated between the Eastern Mediterranean SSTA (16°–38° E; 30°–40° N) and the Sahel (20° W–20° E; 10°–20° N) rainfall above the 75th percentile (see details in the text). Cross-validated skill scores are shown for monthly lagged SSTA regarding August (AUG) precipitation: (a–c) AUG (lag 0), (d–f) JUL (lag 1), (g–i) JUN (lag 2), (j–l) MAY (lag 3) and (m–o) APR (lag 4). RMSE values in the middle (right) column are calculated from non-standardized (standardized) fields. Black stippled regions denote statistically significant values at 95% (0.05) according to a Monte Carlo test (1000 permutations).
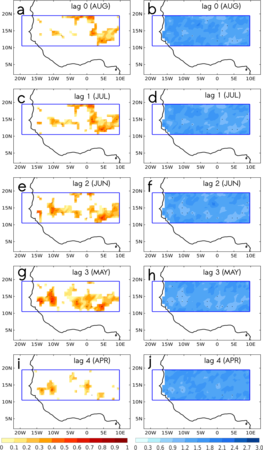
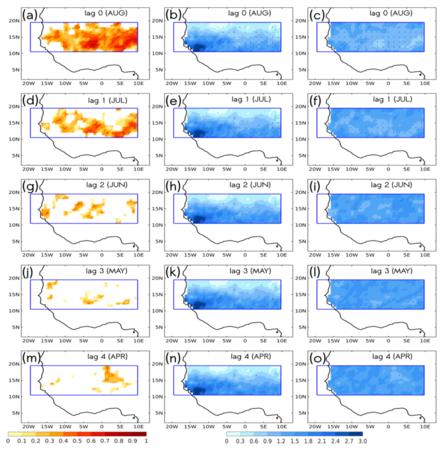
Figure 2 - RIGHT: As in Figure 1 but for the Niño 3.4 region (170°–120° W; 6° S–6° N) that is considered for MCA, and also only the RMSE from the standardized fields are represented. (a,b) AUG (lag 0), (c,d) JUL (lag 1), (e,f) JUN (lag 2), (g,h) MAY (lag 3) and (i,j) APR (lag 4)
**********************************************************************************************************************************************************************************************************
PREDICTION OF TOTAL SAHEL PRECIPITATION DURING THE MONSOON SEASON
Extracted from Suárez-Moreno et al. (2018)
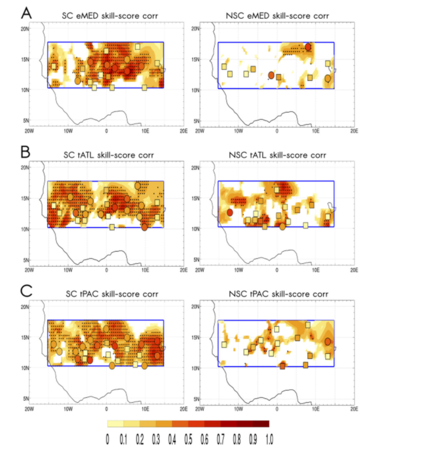
Figure 3: Skill scores between cross-validated hindcasts and observations of rainfall calculated in terms of Pearson correlation coefficients for each grid point in the Sahel (15°W–15°E, 10°–18°N). The analysis is based on the leading MCA modes as indicated in the text. Colored-shaded values correspond to HadISST–CRU analysis. Squares and circles correspond to HadISST–station analysis. Black stippled regions are statistically significant at 95% according to a Monte Carlo test (1000 permutations). Circles (squares) indicate significant (nonsignificant) values for HadISST–station analysis at 95% under a Monte Carlo test (1000 permutations). Cross validation is applied from the MCA between JAS Sahel rainfall and JAS SSTA for (a) eMED, (b) tATL, and (c) tPAC. Skill scores are shown for the (left) SC and (right) NSC periods.
**********************************************************************************************************************************************************************************************************
DYNAMIC PREDICTION OF SAHEL SEASONAL RAINFALL
Extracted from Martin-Gómez et al. (2021, in review)
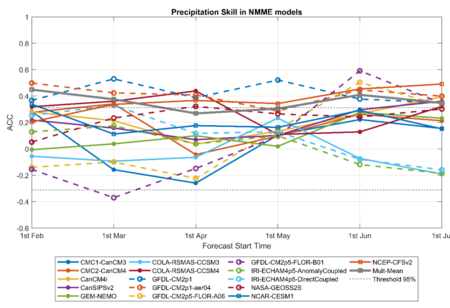
Figure 4: Precipitation prediction skill of the NMME models for different FST. Yellow with squares curve represents the models ensemble mean. The horizontal black dot lines represent values exceeding the 95% confidence level from one tailed t-test. Note that FST = 1st July correspond to lead time 0. ACC values are computed considering precipitation index from GPCPv2.3. Results are similar considering precipitation from CRU TS 4.03 (not shown).
**********************************************************************************************************************************************************************************************************
DECADAL PREDICTION OF SURFACE TEMPERATURE IN SPAIN
Extracted from Gómara et al. (2021 in preparation)
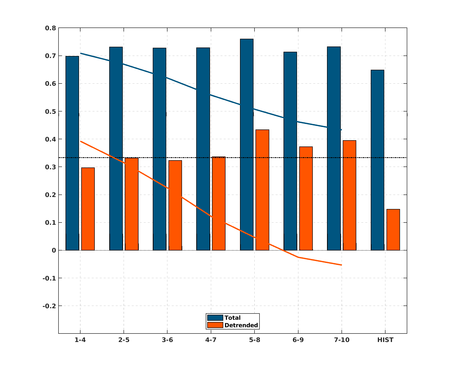
Figure 5: Prediction skill: anomaly correlation coefficients (ACC, adimensional, bars) for Spain's summer (JJA) mean surface temperature at different lead times (1–4, 2–5, 3–6, 4–7, 5–9, 6–9 and 7–10: seven first columns, respectively) in the decadal hindcast and in the historical uninitialized simulation (last column) for raw (dark blue) and de-trended data (orange) in the 1914–2004 period. The detrended scores are calculated over the same time series as the raw ones except that the linear trends are previously removed. Note that the detrended time series cannot be calculated in real-time prediction. Solid lines indicate the ACC skill of persis-tence for raw (dark blue) and detrended data (orange). Persistence is calculated as the average over the 4 years preceding the model ini- tialization. The dot-dashed line show the threshold to reject the null hypothesis that the correlations come from chance (at the 5% level) for 4-year running mean filtered data. Reference data is CRUTS4.03 mean surface temperature estimates estimates.
**********************************************************************************************************************************************************************************************************
PREDICTION OF MALARIA INCIDENCE IN THE SAHEL USING SST INFORMATION FROM DIFFERENT BASINS
Extracted from Diouf et al. (2021)
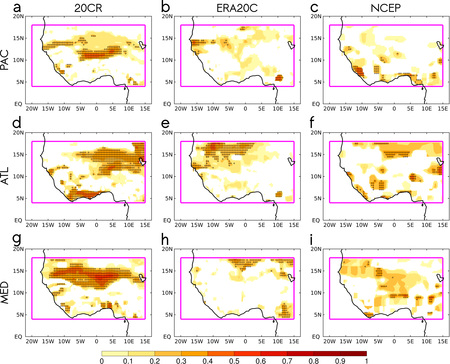
Figure 6: Skill-score validation using Pearson correlation coefficients between observations and hindcasts (modelled malaria incidence under the S4CAST using Atlantic SSTs) for each point in space corresponding to SC period. Significant values are plotted from a 90% statistical significance under a Monte Carlo test.